浮点值应该是我们比较熟悉的一种数据类型，工作中经常用到，会进行比较、计算、转换等等，这些数值操作往往隐藏着很多陷阱，有的可能对计算值产生微小偏差而被忽略，有的可能造成重大软件事故

前言

浮点值应该是我们比较熟悉的一种数据类型，工作中经常用到，会进行比较、计算、转换等等，这些数值操作往往隐藏着很多陷阱，有的可能对计算值产生微小偏差而被忽略，有的可能造成重大软件事故。

什么是浮点

浮点，英文float point，其字面意义就是可以漂移的小数点(浮动的小数点)，来表示含有小数的数值。

我们在数学运算中，经常会遇到无限小数，如1/3=0.333333....无限循环，然而计算机存储容量是有限的，需要舍弃掉一些精度，存储近似值。

浮点在计算机中存储

以前不同CPU的浮点表示方式是不同的，这就导致了机器之间的兼容性问题，后来英特尔发布了8087浮点处理器，被IEEE采用，成为业界的标准，被几乎所有CPU采用(有的GPU除外)。

IEEE754定义了浮点的存储格式，如何取舍(rounding mode)，如何操作(加减乘除等)以及异常处理标准(异常发生的时机与处理方式)。

为了简单起见，我们只看float32，float64及其他，原理都一样。

float32是使用32位来表示浮点数的类型，主要有三个部分

sign，符号位： 1bit，0是负数，1是正数
exponent，指数部分： 8bit，以2为底的指数，
fraction，有效数部分： 23bit，实际表示24bit数值，浮点数具体的数值，

图来自维基百科

所以，一个浮点值可以表示为 \[ sign \times fraction \times 2^{exponent} \] 符号位

符号位1个bit，0表示负数，1表示正数。

指数

IEEE754标准规定固定值为 \[ 2^{e-1} - 1 \] e为指数位数的长度。

单浮点为8位，所以是2^(8-1) - 1=127，而此值是有符号数，所以范围是[-127, 128]，而规定-127和128作为特殊用途，所以真正的有效范围取值是[-126, 127] 指数是-127时的二进制是：00000000，表示指数-127，即2^-127，特殊用途，表示非正规化，后面详细说明指数是-1时的二进制是：01111110，表示指数-1，即2^-1 指数是0时的二进制是：01111111，表示指数0，即2^0 指数是1时的二进制是：10000000，表示指数1，即2^1 指数是127时的二进制是：11111110，表示指数127，即2^127 指数是128时的二进制是：11111111，表示指数128，即2^128，表示无穷大所以指数位是以01111111作为偏移中心点的，称为bias，所以当指数位为127时，则exponent时0。

采用符号位+指数(实际值加上固定的偏移)+有效位数的存储方式，好处是可以用固定bit的无符号整数来表示所有的指数值，所以就可以按照字典比较两个浮点值的大小。例如，我们在自研数据库实现中，如果索引是浮点值，则对正浮点数编码时直接按照IEEE标准的bit存储方式进行编码，这样天然就是有序的。

正规化

采用科学计数法的形式，如果浮点的指数部分在 0 < exponent <= 2^e - 2之间，且有效部分最高有效位是1,那么这种浮点数是正规形式的。

所以浮点值表示为 \[ (-1)^{sign} \times 1.m \times 2^{e-c} \]

m是mantissa，即可以认为是fraction
e是exponent
c是 e最大值的一半

e能表示的最大值是255，一半则是127。所以c是127。第一个有效数字是1，但是其实1没有必要存储，所以就会省略掉，所以23bit能表示24bit的值。

那我们将10.1转成正规化浮点，整数10的二进制是：1010，小数0.1，十进制小数转二进制，是将小数值转成2^-1到2-E的和的形式(二进制，所以相当于除以2)，如

\[ 0.1 = 2^{-4} + 2^{-5} + 2^{-8} + 2^{-9} + 2^{-12} + 2^{-13} + 2^{-16} + 2^{-17} + 2^{-19}...... \] 无法除尽，有效位24bit，所以二进制为1010.00011001100110011010 \[ 1.01000011001100110011010 \times 2^{3} \] 再将其正规化，小数点前保留一位，1可以省略 \[ 01000011001100110011010 \times 2^{3} \] 指数位2^(e-c)，2³⁼²(130-127)`，所以是10000010, 符号位是0，所以10.1的二进制表示为：01000001001000011001100110011010

使用转换工具

非正规化

正规化能存储最小的正数值是 \[ sign \times 1.m \times 2 ^ {-126} \] 当指数和有效数都是0是，就是数学上的0，然而如果指数是0，有效数不是0，则称为underflow，意思非常接近于0，无法用正规的浮点来表示，这种就称为非正规化浮点。

非正规浮点值表示为： \[ (-1) ^ {sign} \times 0.m \times 2 ^ {(-c + 1)} \] 有效数最高位位是0，所以可以用来存储更接近于0的数字。(-c+1)等于-126，指数和正规化一样小，但由于最高位可以是0，所以在有效位上，能表示更小的小数值，精度多了22位。

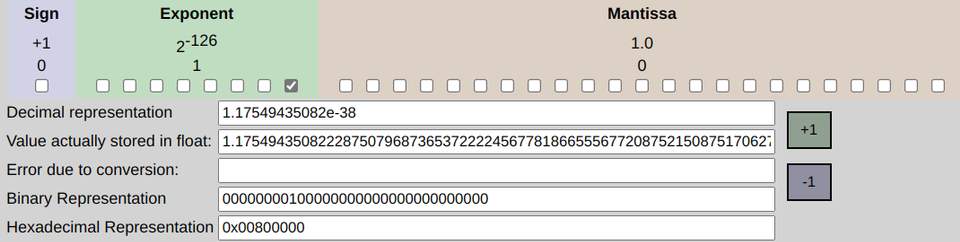
我们看下正规化最小正数

再看看非正规化最小正数

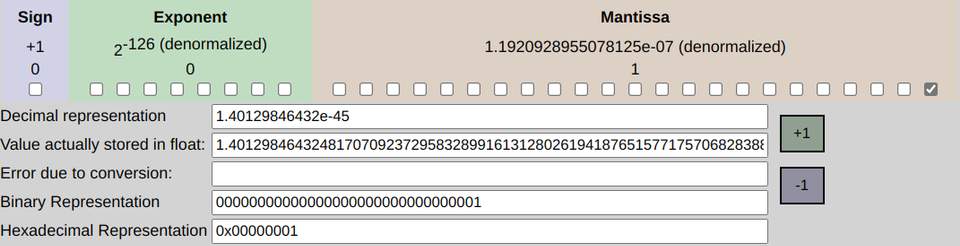
可以看出有效位数非正规化精度多了22位，最小值十进制从正规化的1.17 x e^-38变成非正规化的1.4 x e^-45。

特殊值

IEEE标准还规定了一些浮点的特殊值

浮点	指数	有效数字
0	0	0
非正规	0	非0
正规	1 < x < 2^(e-2)	1 <= x < 2
无穷	2^(e-1)	0
NaN	2^(e-1)	非0

NaN表示not a number，没有意义的值，如0/0, sqrt(-1)。

浮点的精度

数学上是否可以用有限的数字来表示一个有理数，取决于其基数。如，对于基数是10，1/2可以表示为0.5，而1/3则表示为0.333333.....，无法用有限数字表示。
而对于基数是2来说，只有分母是2的倍数的数才可以被有限数字表示；任何其他分母不是以2为倍数的，则无法用有限数字表示。所以对于这种数字，则无法"准确"转换成10进制。
例如十进制0.1，转换成二进制则无法用有限数字表示，需要截断，就造成精度丢失而产生计算过程中的误差。

由于浮点的表示是 \[ (-1)^{sign} \times n.m \times 2^{exponent} \] 既然是有效数乘以指数，那么其精度会随着数值越大而降低。

如浮点1的二进制是00111111100000000000000000000000，而正规化所能表示的1的下一个浮点值是00111111100000000000000000000001(有效位最后一位改成1)，是1.00000011921，两者相差0.00000011921。浮点10000的二进制是01000110000111000100000000000000，而其下一个浮点值是01000110000111000100000000000001，十进制为10000.0009766，两者相差0.0009766，可见，其精度降低了几个数量级。

我们来打印1到10亿量级递增的浮点值精度，即每个量级的值和它浮点所能表示的下一个浮点值。

float a = 1.0;
for (int i = 0; i < 10; i++)
{
    uint32_t b = reinterpret_cast<uint32_t&>(a) + 1;
    float c = reinterpret_cast<float&>(b);
    printf("%32.20f - %32.20f = %2.20f\n", c, a, c - a);
    a *= 10;
}

可以看出，浮点1和其下一个浮点值差为0.00000011920928955078，而浮点1000000000和其下一个浮点值的差为64。

所以随着浮点值越大，其精度也越低。

         1.00000011920928955078 -           1.00000000000000000000 = 0.00000011920928955078
        10.00000095367431640625 -          10.00000000000000000000 = 0.00000095367431640625
       100.00000762939453125000 -         100.00000000000000000000 = 0.00000762939453125000
      1000.00006103515625000000 -        1000.00000000000000000000 = 0.00006103515625000000
     10000.00097656250000000000 -       10000.00000000000000000000 = 0.00097656250000000000
    100000.00781250000000000000 -      100000.00000000000000000000 = 0.00781250000000000000
   1000000.06250000000000000000 -     1000000.00000000000000000000 = 0.06250000000000000000
  10000001.00000000000000000000 -    10000000.00000000000000000000 = 1.00000000000000000000
 100000008.00000000000000000000 -   100000000.00000000000000000000 = 8.00000000000000000000
1000000064.00000000000000000000 -  1000000000.00000000000000000000 = 64.00000000000000000000

不准确的浮点

除了前面说的精度问题外，还有以下情况会导致浮点"不准确"

类型转换
算术运算
进制转换

类型转换

一般情况下，我们都知道类型转换可能导致精度丢失，但还有一些其他情况也会导致数值不准确。

如下

float a = 0.1;
double b = a;
double c = 0.1;

printf(b == c ? "b=c\n" : "b!=c\n");

输出结果是

b!=c

由于b=a赋值是直接将a按照bit转换成b，并不是将0.1转换为b，所以其有效数的精度是和float一样的。而double c = 0.1的精度却比float高很多，所以造成两者并不相等。

算术运算

浮点值只要经过运算，就可能不符合数学的运算性质，如结合律、分配律等。

如(0.1/10)*10不等于0.1。

如下例子 \[ x^{2} + 200x - 10.0025 = 0 \] 求得x的值 \[ \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \] 我们自己计算得出x的值是：0.05, -200.05

但我们通过在程序中用浮点计算得出是：0.050003051757812，-200.050003051757812，0.05与0.050003051757812不相等。

进制转换

前面讨论过进制转换可能导致精度丢失。

浮点比较

既然浮点存储会精度丢失，那么使用浮点进行比较、计算等都需要考虑精度的丢失以及精度偏差的累计等等问题。

而我们使用最多的应该还是对浮点进行比较，那么我们就来了解下浮点该如何进行比较。

直接比较

在没有了解浮点前，可能大部分人都会这么比较

bool equal(float a, float b)
{
    return a == b;
}

前面我们讨论过，浮点有精度问题，所以如果a精度丢失了，那么和b则不相等。

Epsilon

我发现很多文章介绍浮点比较是这样的，我也在不少代码中见过此类用法。

// FLT_EPSILON is equal to the difference between 1.0 and the value that follows it.
#define FLT_EPSILON 1.19209290E-07F // decimal constant

bool equal(float a, float b)
{
    return fabs(a - b) <= FLT_EPSILON;
}

前面我们讨论过由于随着浮点值越大，其精度会越低，而epsilon是1和1后一个浮点值的差值，所以当浮点值大于1时，这样比较就不正确。

Relative epsilon

那我们是否可以通过根据浮点数大小来缩放差值呢？代码如下：

bool equal(float a, float b, float diff = FLT_EPSILON)
{
    return fabs(a - b) / std::min(fabs(a), fabs(b)) < diff;
}

这种方式正确吗？

我们使用前面的方程 \[ x^{2} + 200x - 10.0025 = 0 \] 求得值为0.050003051757812，-200.050003051757812，而我们期望的是0.05, -200.05。
按照此函数比较值0.05和0.050003051757812，计算fabs(a - b) / std::min(fabs(a), fabs(b))是0.00006102025508880615234375，如果diff使用FLT_EPSILON，则返回false。

ULPs（units of least precision）最小精度单元

如果知道某个浮点值和其后一个浮点值的差值，就可以通过fabs(a-b) < ULPs(a)这个差值来判断是否相等。
我们称这个差值为最小精度单元 units of least precision。

我们知道了浮点按照IEEE标准的存储方式，那么就可以按照bit位相减的方式来计算浮点值之间有多少个最小精度单元。

bool equal(float a, float b, int ulpsEpsilon)
{
    ulsp(a, b) < ulpsEpsilon;
}

int ulsp(float a, float b)
{
    int32_t ia = reinterpret_cast<int32_t&>(a);
    int32_t ib = reinterpret_cast<int32_t&>(b);
    int32_t distance = ia - ib;
    if (distance < 0) distance = -distance;
    return distance;
}

那我们来比较前面的方程，比较 \[ x^{2} + 200x - 10.0025 = 0 \] 其值0.0500030517578125与0.05的ULPs是819！！
而在计算前，我们又怎么知道用一个多大的ulpsEpsilon合适呢？

回归本质

前面讨论了几种比较方法，那么到底用哪一种方式比较浮点呢？
其实，并没有一个统一的答案，要视不同的情况而定。

我们先回顾前面的直接比较方法：return a == b;。

这种方法真的不正确吗？
其实，只要不进行类型转换、运算等，就不会有问题！

假如，我们将浮点写入一个文件，后面再读入此浮点进行比较是否有更改，只要写入文件时按照bit位写入文件，那么就不会有问题！

再看return fabs(a - b) <= FLT_EPSILON;，如果a和b都小于1，则这种方法也没有问题。

至于ULPs，其相对比较准确，但是，浮点经过一系列计算后，我们无法知道浮点精度丢失了多少，该选择一个多大ulpsEpsilon。所以一个浮点经过大量计算后，我们所期望他的精度最多丢失多少，那么就选择一个多大的ulpsEpsilon。

最后是relative_epsilon，此函数计算一个相对的epsilon，相对于两个比较的浮点而言，他们的差与其值的比。同样，对于一个经过大量计算的浮点，如果它的值与我们期望的值的误差(丢失的精度)在此浮点值中的比不大于多少就表示两者相等，则可以使用relative_epsilon。
例如，浮点值0.05与0.0500030517578125的ULPS是819，而relative epsilon是0.00006102025508880615234375，可见其误差在0.05的占比是非常低的，如果我们能接受这种占比的误差，就可以选择relative epsilon的比较方式。

前面用了很多比较方法，但都没有考虑浮点的特殊值，一个正确的比较函数应该考虑这些情况，如下，我们完善ULPS的比较。

bool equal(float a, float b, int ulpsEpsilon)
{
    ulps(a, b) < ulpsEpsilon;
}

int32_t ulps(float a, const float b)
{
    // 相等，则直接返回
    if (a == b) return 0;

    const auto max = std::numeric_limits<int32_t>::max();
    
    // 判断是否是NaN
    if (isnan(a) || isnan(b)) return max;
    if (isinf(a) || isinf(b)) return max;

    int32_t ia = reinterpret_cast<int32_t&>(a);
    int32_t ib = reinterpret_cast<int32_t&>(b);

    // 符号位不同
    if ((ia < 0) != (ib < 0)) return max;

    int32_t distance = ia - ib;
    if (distance < 0) distance = -distance;
    return distance;
}

最后

不知有多少老司机在浮点值上踩过坑，有的甚至造成重大的事故，甚至灾难。

从文中我们了解了浮点存储原理，精度丢失问题，以及如何进行比较，希望能给大家带来帮助。